H
E
E
L
E
M
E
N
T
S
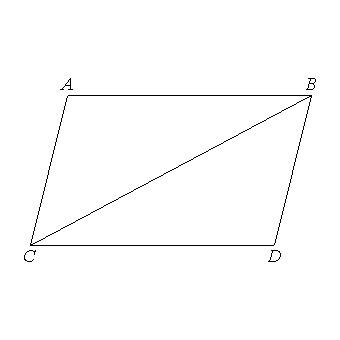
the side AB is equal to the side CD, and the side AC to BD;
and further
the angle BAC is equal to the angle CDB.
And, since
the angle ABC is equal to the angle BCD, and the angle CBD to the angle ACB,
the whole angle ABD is equal to the whole angle ACD. [C.N.2]
Therefore in parallelogrammic areas
the opposite sides and angles are equal to one another.
Being (part of) what it was required to prove.