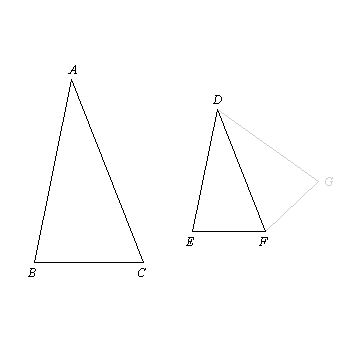H
E
E
L
E
M
E
N
T
S
on the straight line DF, and at the points D, F on it,
let there be constructed the angle FDG equal to either of the angles BAC, EDF,
and
the angle DFG equal to the angle ACB; [I.23]
therefore
the remaining angle at B is equal to the remaining angle at G. [I.32]
Therefore
the triangle ABC is equiangular with the triangle DGF.