H
E
E
L
E
M
E
N
T
S
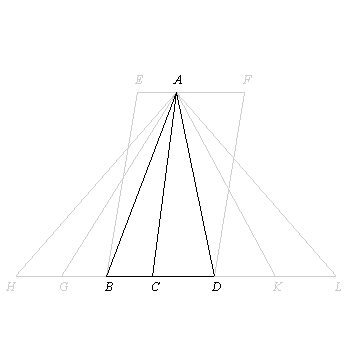
two bases BC, CD and two triangles ABC, ACD, equimultiples have been taken
of the of the base BC and the triangle ABC, namely
the base HC and the triangle AHC,
and of the base CD and the triangle ADC other, chance, equimultiples, namely
the base LC and the triangle ALC;
and it has been proved that,
if the base HC is in excess of the base CL,
the triangle AHC is also in excess of the triangle ALC;
if equal, equal; and
if less, less.
Therefore
as the base BC is to the base CD,
so is the triangle ABC to the triangle ACD. [V.Def.5]