H
E
E
L
E
M
E
N
T
S
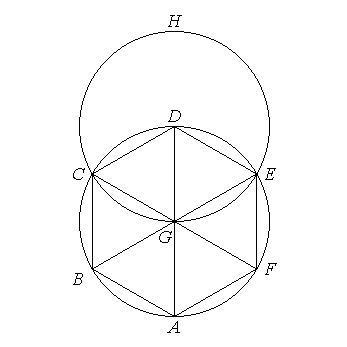
From this it is manifest that the side of the hexagon is equal to the radius of the circle.
And, in like manner as in the case of the pentagon, if through the points of division on the circle we draw tangents to the circle, there will be circumscribed about the circle an equilateral and equiangular hexagon in conformity with what was explained in the case of the pentagon.
And further, by means similar to those explained in the case of the pentagon, we can both inscribe a circle in a given hexagon and circumscribe one about it.