H
E
E
L
E
M
E
N
T
S
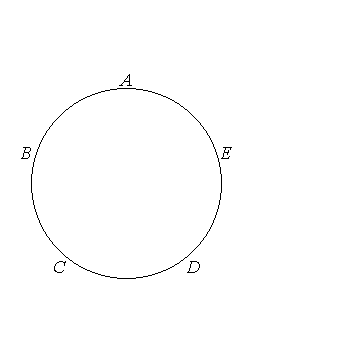
let there be inscribed in the circle ABCDE the triangle ACD equiangular with the triangle FGH, so that the angle CAD is equal to the angle at F and the angles at G, H respectively equal to the angles ACD, CDA; [IV.2]
therefore each of the angles ACD, CDA is also double of the angle CAD.
Now
let the angles ACD, CDA be bisected respectively by the straight lines CE, DB, [I.9]
and
let AB, BC, DE, EA be joined.