T
H
E

E
L
E
M
E
N
T
S		 Book IV   Proposition 10
Then, since the rectangle AB, BC is equal to the square on AC, and
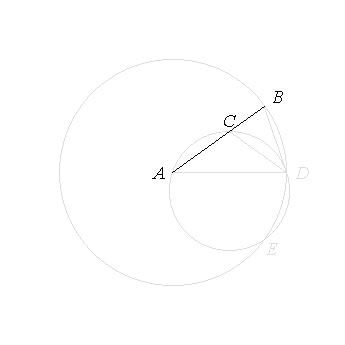
    AC is equal to BD,
therefore
    the rectangle AB, BC is equal to the square on BD.

And, since
    a point B has been teken outside the circle ACD,
and from B
    the two straight lines BA, BD have fallen on the circle ACD, and one of them cuts it, while the other falls on it,
and
    the rectangle AB, BC is equal to the square on BD,
therefore
    BD touches the circle ACD. [III.37]
Previous Page    Return to Propositions    Next Page