H
E
E
L
E
M
E
N
T
S
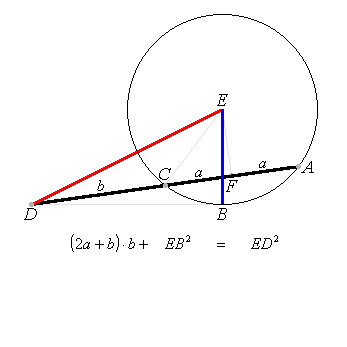
the squares on EB, BD are equal to the square on ED,
for the angle EFC is right; [I.47]
therefore
the rectangle AD, DC together with the square on EB is equal to the squares on EB, BD.
Let the square on EB be subtracted form each;
therefore
the rectangle AD, DC which remains is equal to the square on DB.
Being what it was required to prove