H
E
E
L
E
M
E
N
T
S
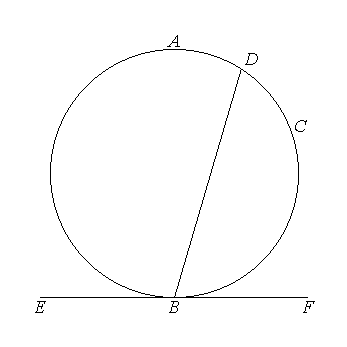
if a straight line EF touch the circle ABCD at the point B, and from B there is drawn across, in the circle ABCD, a straight line cutting it,
then
the angle FBD is equal to the angle constructed in the segment BAD,
and
the angle EBD is equal to the angle constructed in the segment DCB.
Being what it was required to prove.