T
H
E

E
L
E
M
E
N
T
S		 Book III   Proposition 32
For let a straight line EF touch the circle ABCD at the point B, and from the point B let there be drawn across, in the circle ABCD, the straight line BD cutting it;

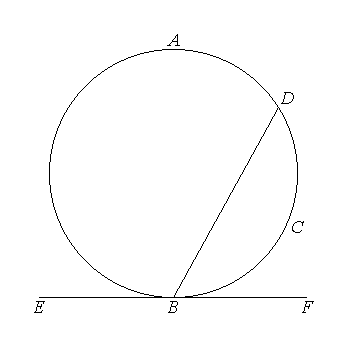
I say that the angles which BD makes with the tangent EF will equal to the angles in the alternate segments of the circle, that is, that
    the angle FBD is equal to the angle constructed in the segment BAD,
and
    the angle EBD is equal to the angle constructed in the segment DCB.
Return to Propositions    Next Page