T
H
E

E
L
E
M
E
N
T
S		 Book III   Proposition 14
Next, let the straight lines AB, CD be equally distant from the center; that is, let EF be equal to EG.

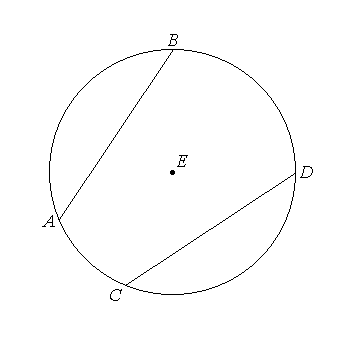
I say that AB is also equal to CD.

For,
    with the same construction,
we can prove, similarly, that
    AB is double of AF, and CD of CG.
And, since AE is equal to CE,
    the square on AE is equal to the square on CE.
But
    the squares on AF, FE are equal to the square on AE,
and
    the squares on CG, GE equal to the square on CE. [I.47]
   Previous Page   Return to Propositions   Next Page