H
E
E
L
E
M
E
N
T
S
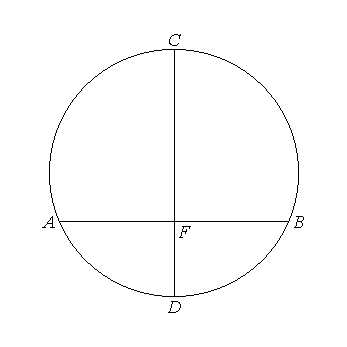
since EA is equal to EB,
the angle EAF is also equal to the angle EBF.
But the right angle AFE is equal to the right angle BFE, therefore
EAF, EBF are two triangles having two angles equal to two angles and one side equal to one side, namely EF, which is common to them, and subtends one of the equal angles;
therefore they will also have the remaining sides equal to the remaining sides; [I.26] therefore
AF is also equal to FB.