H
E
E
L
E
M
E
N
T
S
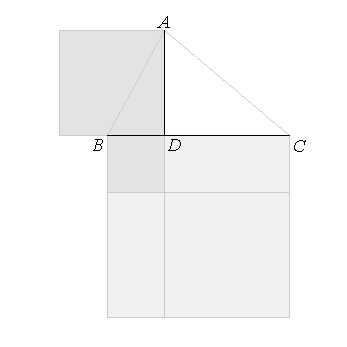
the square on AB is equal to the squares on BD, DA, for the angle at D is right; [I.47]
and
the square on AC is equal to the squares on AD, DC;
therefore
the squares on AB, BC
are equal to
the square on AC and twice the rectangle CB, BD,
so that
the square on AC alone is less than the squares on AB, BC by twice the rectangle contained by CB, BD.
Being what it was required to prove.