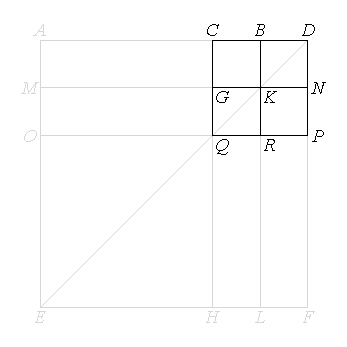H
E
E
L
E
M
E
N
T
S
BC is equal to BD, and GK to KN,
therefore
CK is also equal to KD, and GR to RN. [I.36]
But
CK is equal to RN, for they are complements of the parallelogram CP; [I.43] therefore
KD is also equal to GR;
therefore
the four areas DK, CK, GR, RN are equal to one another.
Therefore
the four are quadruple of CK.