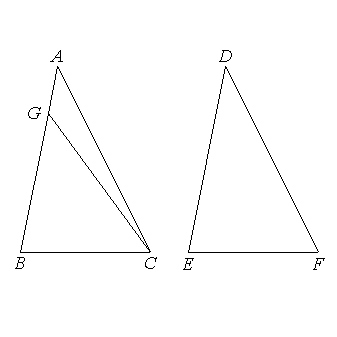T H E E L E M E N T S	Book I   Proposition 26
	Then, since BG is equal to DE, and BC to EF,     the two sides GB, BC are equal to the two sides DE, EF respectively; and the angle GBC is equal to the angle DEF;     therefore the base GC is equal to the base DF, and the triangle GBC is equal to the triangle DEF, and thr remaining angles will be equal to the remaining angles, namely those which the equal sides subtend; [I.4] therefore     the angle BCG is equal to the angle EFD. But     the angle EFD is by hypothesis equal to the angle BCA; therefore     the angle BCG is equal to the angle BCA, the greater to the less: which is impossible. Therefore AB is not unequal to DE, and is therefore equal to it.
	Previous Page    Return to Propositions    Next Page