H
E
E
L
E
M
E
N
T
S
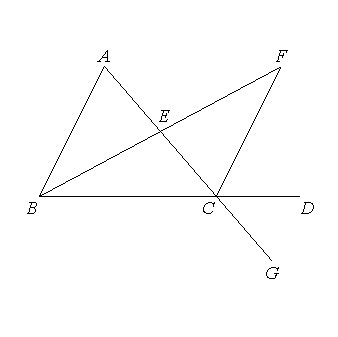
the two sides AE, EB are equal to the two sides CE, EF respectively;
and the angle AEB is equal to the angle CEF, for they are vertical angles, [I.15]
Therefore
the base AB is equal to the base FC, and the triangle AEB is equal to the triangle CEF, and the remaining angles are equal to the remaining angles respectively, namely those which the equal sides subtend; [I.4]
therefore
the angle BAE is equal to the angle ECF.