H
E
E
L
E
M
E
N
T
S
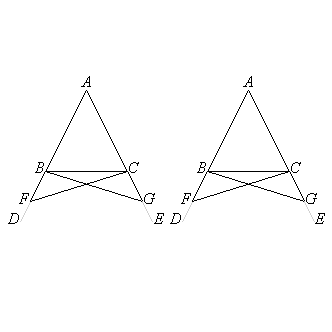
AF is equal to AG, and in these AB is equal to AC,
the remainder BF is equal to the remainder CG.
But FC was also proved equal to GB; therefore
the two sides BF, FC are equal to the two sides CG, GB respectively; and the angle BFC is equal to the angle CGB, while the base is common to them;
therefore
the triangle BFC is equal to the triangle CGB, and the remaining angles will be equal to rhe remaining angles respectively, namely those which the equal sides subtend; thus the angle FBC is equal to the angle GCB, and
the angle BCF to the angle CBG.