H
E
E
L
E
M
E
N
T
S
I say that they will also have the remaining sides equal to the remaining sides respectively, namely AC to DF and BC to EF, and the remaining angle to the remaining angle, namely the angle BAC to the angle EDF.
|
T H E E L E M E N T S |
Book I Proposition 26 | |
|
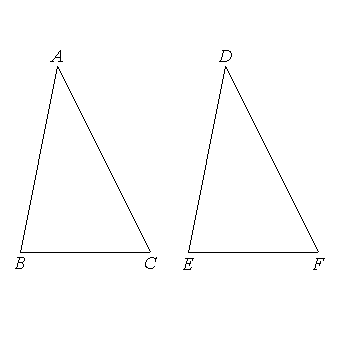
Let ABC, DEF be two triangles having the two angles ABC, BCA equal to the two angles
DEF, EFD respectively, namely
the angle ABC to the angle DEF,
and
the angle BCA to the angle EFD;
and let them also have one side equal to one side, (now let it be) a side subtending equal angles, as
AB to DE. I say that they will also have the remaining sides equal to the remaining sides respectively, namely AC to DF and BC to EF, and the remaining angle to the remaining angle, namely the angle BAC to the angle EDF. |

|
|
| Previous Page Return to Propositions Next Page | ||