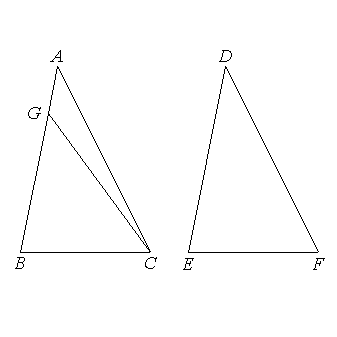H
E
E
L
E
M
E
N
T
S
the two sides GB, BC are equal to the two sides DE, EF respectively; and the angle GBC is equal to the angle DEF;
therefore the base GC is equal to the base DF, and the triangle GBC is equal to the triangle DEF, and thr remaining angles will be equal to the remaining angles, namely those which the equal sides subtend; [I.4] therefore
the angle BCG is equal to the angle EFD.
But
the angle EFD is by hypothesis equal to the angle BCA;
therefore
the angle BCG is equal to the angle BCA,
Therefore AB is not unequal to DE,