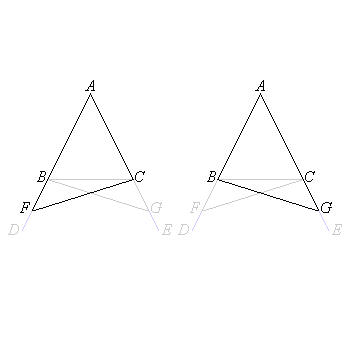T H E E L E M E N T S	Book I   Proposition 5
	It was shown that BF is equal to CG and FC is equal to GB. So, since     the two triangles have the two sides BF, FC equal to the two sides CG, GB respectively, and the angle BFC of the one equal to the angle CGB of the other, [then also]     the base CB is common with itself and     the triangle BFC will be equal to the triangle CGB and     the remaining angles will be equal to the remaining angles respectively, those the equal sides subtend. Therefore     the angle FBC is equal to the angle GCB and     the angle BCF is equal to the angle CBG.
	Previous Page    Return to Propositions    Next Page